この記事は2024年5月25日にチーム内Wikiに書かれたレポートを転記したものです.
目的
ロボットの3次元的な重心位置を計測する。
結果
2台,4種類の条件で重心を計測した。
結果は下の表の通り。
位置はボトムプレート下面、外形の円中心が基準。
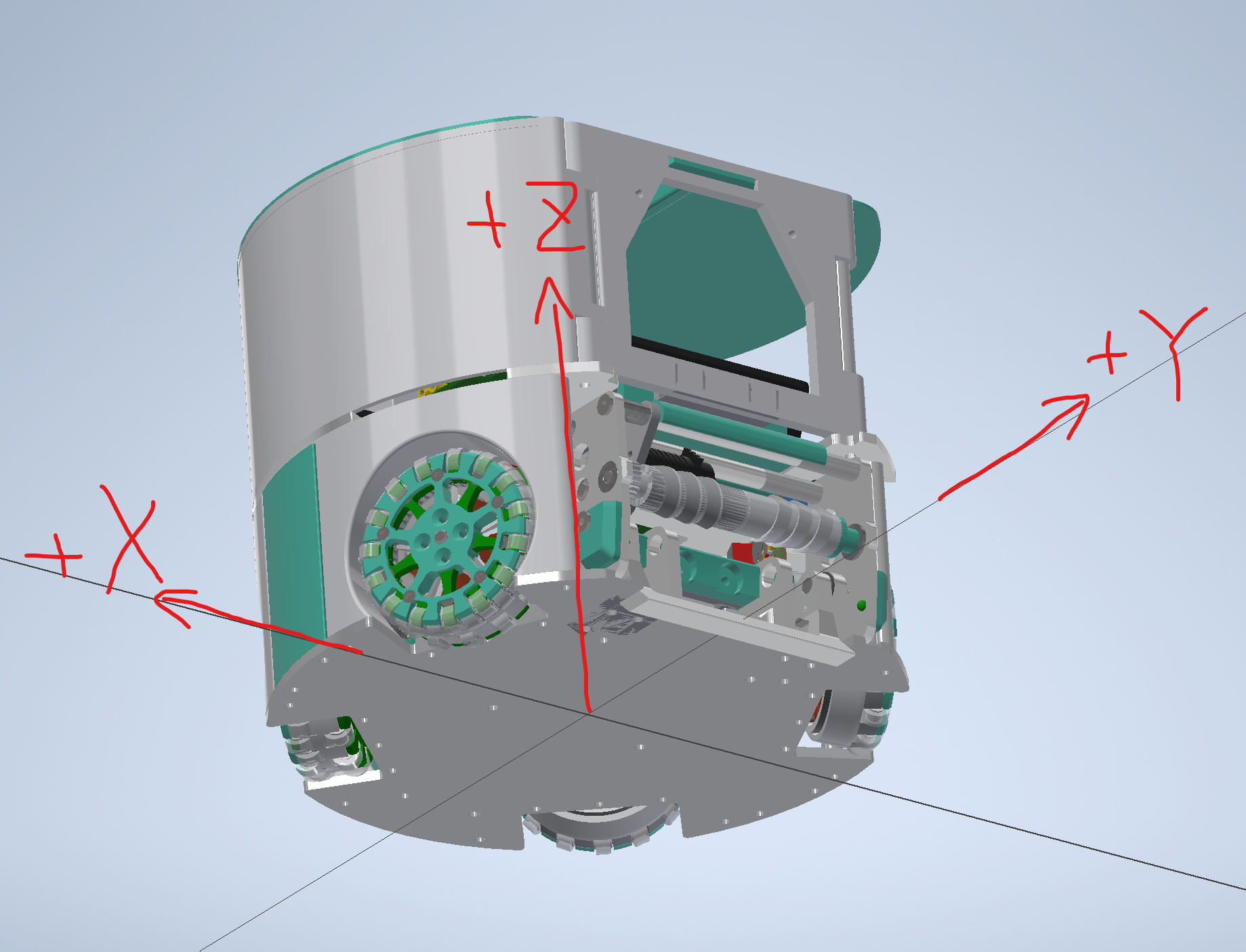
右方向が+X、前方向が+Y、高さ方向が+Z,下図の通り。
リポチェッカー,ラズパイは非搭載。
| ロボット番号 | X | Y | Z |
|---|---|---|---|
| 4 | 1.1 | -8.9 | 47.0 |
| 7 | 2.1 | -8.3 | 46.5 |
| 7(リポなし) | 2.2 | -2.0 | 44.8 |
| 7(リポなし、下半分) | 0.6 | -1.4 | 26.4 |
重心計測の基準位置
測定方法
一度の計測で3次元の重心位置を得ることができないので,
2次元の重心位置を姿勢を変えて数パターン計測する。
2D重心位置の計測
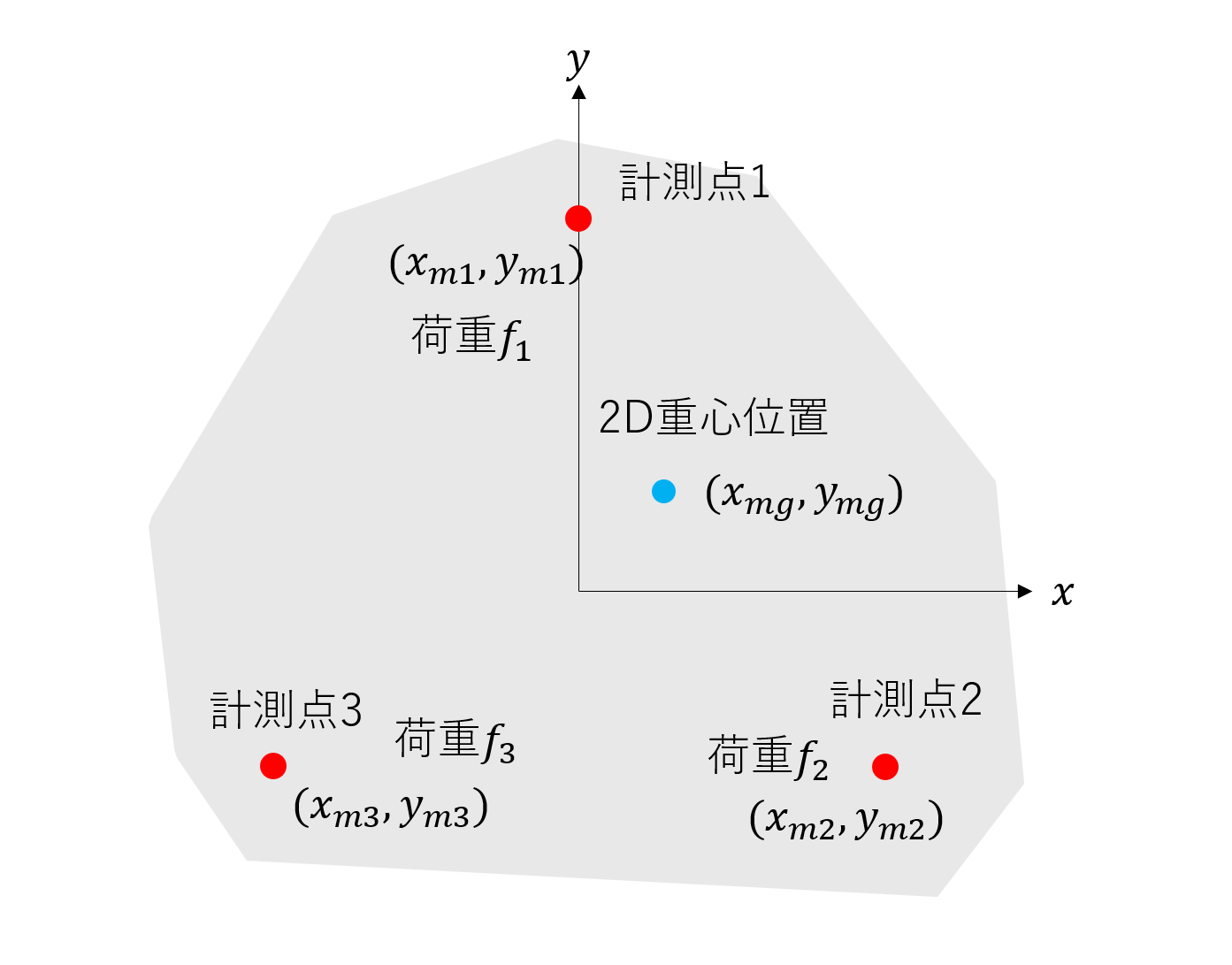
ロボットを3点で支え,その3点の荷重をキッチンスケールで計測する。
計測点の位置と各点の荷重から,水平面に投影された重心位置を得ることができる。

各計測点の位置関係を下図のように定義する。
各計測点の座標を
,投影された重心位置を
それぞれの荷重を
とした。
ロボットが静止していれば,X軸回り,Y軸回りのモーメントはいずれもゼロである。
したがって,
重心位置
について解けば,次の解が得られる。
これで,水平面に投影した重心位置が計測できることがわかった。
3D重心位置の計測
3次元の重心を計測するため,ロボットの姿勢を変えて2Dの重心計測をする。
各記号を以下のように定義する。
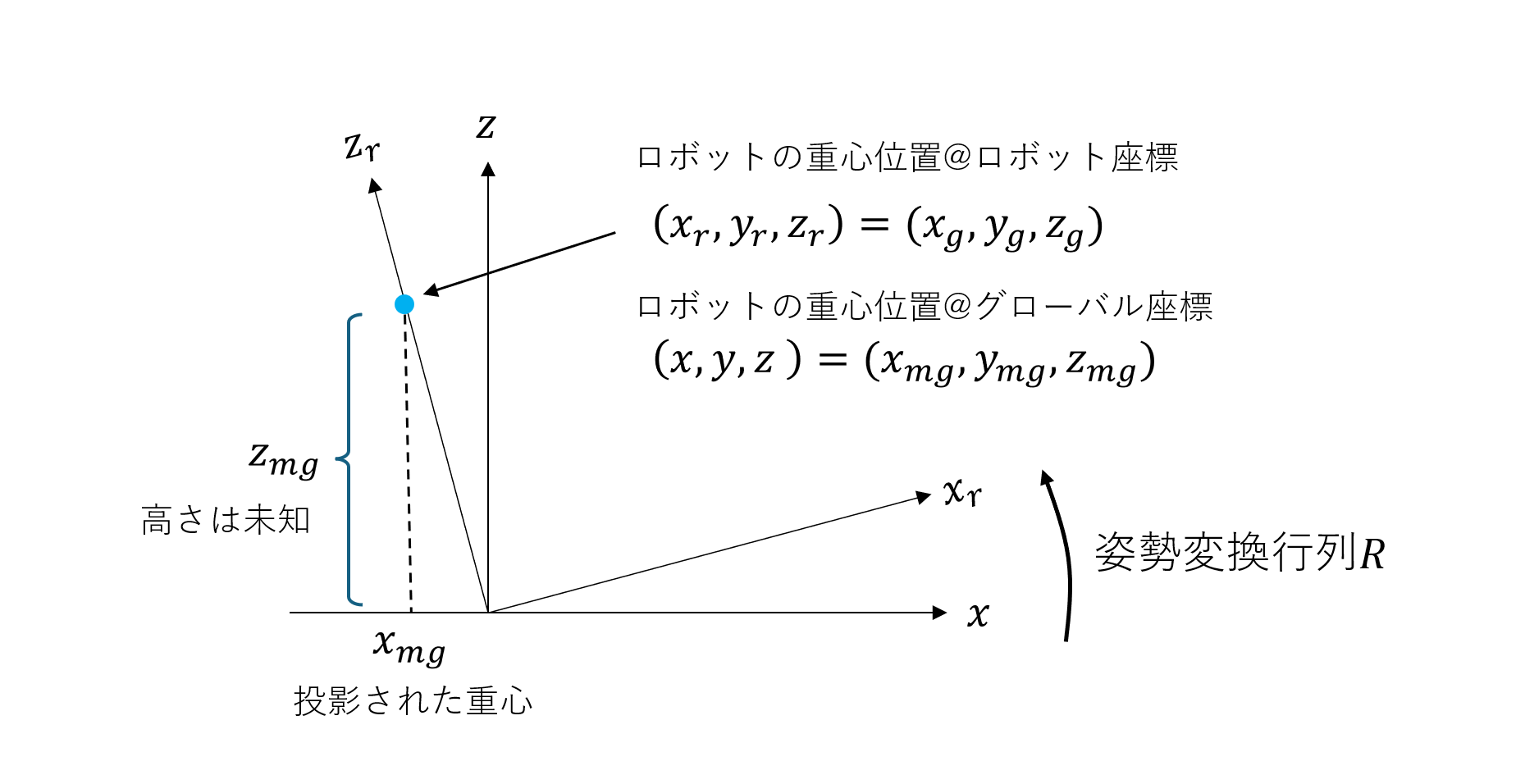
ロボットの姿勢を回転行列Rに従って回転させることで,
重心は次のように移動する。
このうち,観測できるのは
のみであるので,
観測行列Cをかけて取り出す。
これでロボットの姿勢を傾けたときの重心計測を定式化できた。
姿勢を変えた計測は数パターン行う。
Nケース計測を行うとして,この時の姿勢変換行列を
,
それぞれ計測された重心位置を
とした。
次のような線形方程式
を解くことで3次元の重心位置
を求めることができる。
明らかにMは正方行列ではないので,疑似逆行列とか特異値分解でそれらしい値を出せばいいと思う。
MATLABの場合v = M \ wとすることで,QR分解を用いたいい感じの解(たぶん最小二乗解)を出してくれる。
今回の測定パラメータ
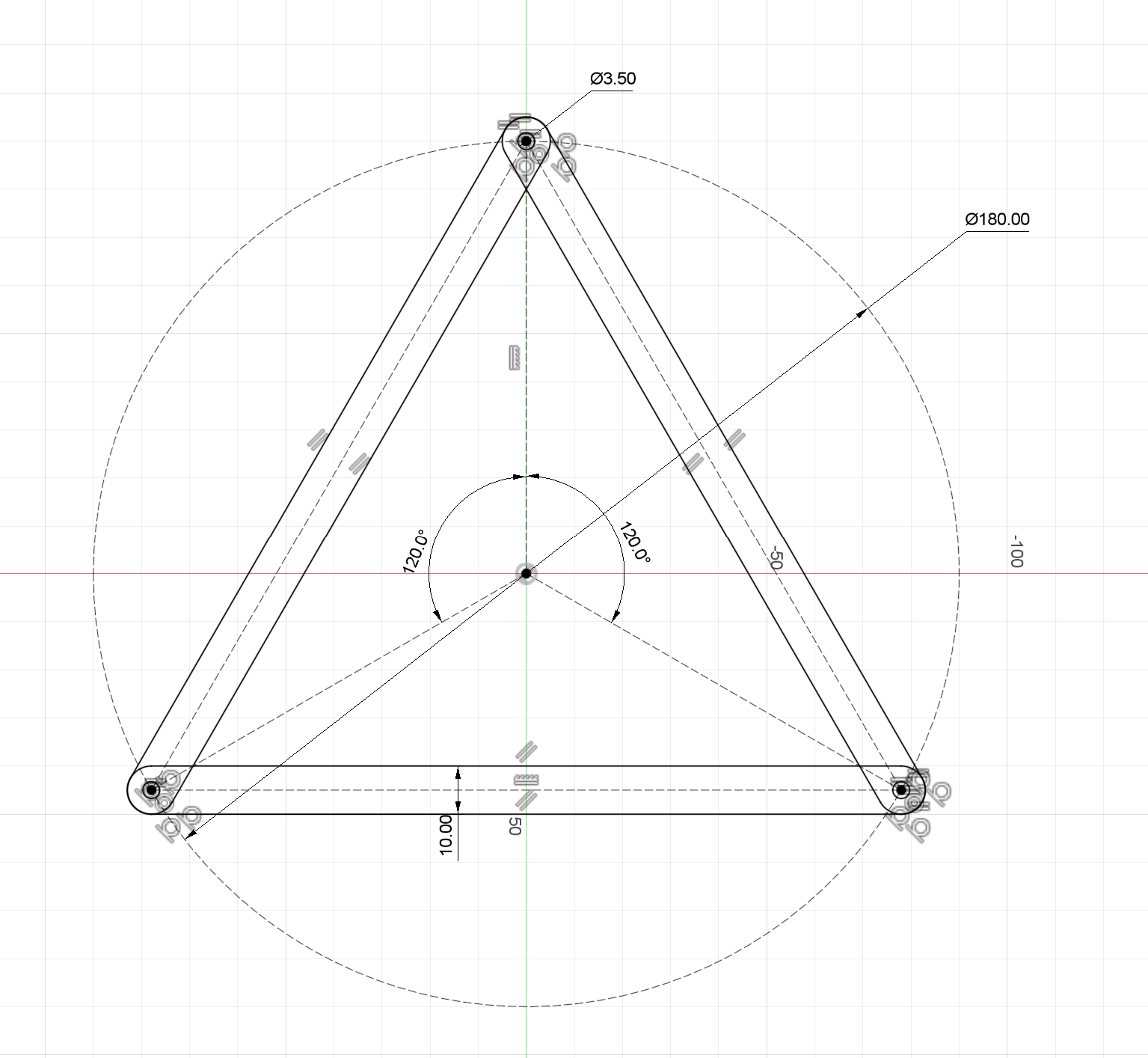
計測点の配置
半径90mm,120度ごとに配置
治具の角度
オイラー角(ZYX),各軸のプラス方向から見て反時計回りを正とする
| 治具No. | Z[deg.] | Y[deg.] | X[deg.] |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 30 |
| 3 | 0 | 15 | 0 |
| 4 | 0 | 0 | -15 |